Công Thức Đạo Hàm: Tổng Hợp Đầy Đủ, Dễ Nhớ Và Dễ Áp Dụng

Trong chương trình Toán học phổ thông, đặc biệt là Toán lớp 11 và 12, công thức đạo hàm là một trong những phần kiến thức quan trọng nhất. Không chỉ xuất hiện dày đặc trong đề kiểm tra, đề thi tốt nghiệp THPT, mà công thức đạo hàm còn là nền tảng cho nhiều chủ đề nâng cao như khảo sát hàm số, cực trị, đồ thị và ứng dụng thực tế.

Vậy công thức đạo hàm là gì, gồm những dạng nào, làm sao để ghi nhớ và áp dụng hiệu quả? Bài viết này sẽ giúp bạn hệ thống đầy đủ – dễ hiểu – dễ học nhất toàn bộ nội dung liên quan đến đạo hàm.
 

Trước khi đi sâu vào công thức đạo hàm, ta cần hiểu rõ khái niệm đạo hàm.

Đạo hàm của một hàm số tại một điểm thể hiện tốc độ thay đổi của hàm số tại điểm đó.

Nói cách khác, đạo hàm cho biết:

• Hàm số đang tăng hay giảm
  

• Độ dốc của tiếp tuyến tại một điểm
  

• Mức độ biến thiên của đại lượng
  

Chính vì vậy, công thức đạo hàm đóng vai trò như “chìa khóa” để giải quyết rất nhiều bài toán khác nhau.
 

Rất nhiều học sinh gặp khó khăn trong Toán học chỉ vì không thuộc hoặc không hiểu công thức đạo hàm. Việc nắm
chắc các công thức mang lại nhiều lợi ích:

• Giải nhanh bài tập trắc nghiệm
  

• Tránh nhầm lẫn khi tính toán
  

• Dễ dàng học các phần nâng cao
  

• Áp dụng tốt trong Vật lý, Kinh tế, Kỹ thuật
  

Có thể nói, công thức đạo hàm là nền tảng không thể thiếu nếu muốn học tốt giải tích.
 

Đây là nhóm công thức đạo hàm quan trọng nhất, bắt buộc phải ghi nhớ.

1. Đạo Hàm Của Hằng Số

• Nếu y=cy = cy=c (c là hằng số)
   👉 y′=0y' = 0y′=0
  

2. Đạo Hàm Của Hàm Lũy Thừa

• Nếu y=xny = x^ny=xn
  y′=n⋅xn−1y' = n \cdot x^{n-1}y′=n⋅xn−1
  

Ví dụ:

• (x2)′=2x(x^2)' = 2x(x2)′=2x
  

• (x3)′=3x2(x^3)' = 3x^2(x3)′=3x2
  

Đây là công thức đạo hàm xuất hiện nhiều nhất trong đề thi.
 

1. Tổng và Hiệu

• (u+v)′=u′+v′(u + v)' = u' + v'(u+v)′=u′+v′
  

• (u−v)′=u′−v′(u - v)' = u' - v'(u−v)′=u′−v′
  

2. Hằng Số Nhân

• (k⋅u)′=k⋅u′(k \cdot u)' = k \cdot u'(k⋅u)′=k⋅u′
  

Nhóm công thức đạo hàm này giúp rút gọn bài toán phức tạp thành các phần nhỏ hơn.
 

Nếu:

y=uvy = \frac{u}{v}y=vu​

Thì:

y′=u′v−uv′v2y' = \frac{u'v - uv'}{v^2}y′=v2u′v−uv′​

👉 Đây là công thức đạo hàm dễ nhầm dấu nhất, học sinh cần đặc biệt cẩn thận.
 

Hàm hợp có dạng:

y=f(g(x))y = f(g(x))y=f(g(x))

Khi đó:

y′=f′(g(x))⋅g′(x)y' = f'(g(x)) \cdot g'(x)y′=f′(g(x))⋅g′(x)

Công thức này thường được gọi là quy tắc dây chuyền – một trong những công thức đạo hàm quan trọng nhất ở mức nâng cao.
 

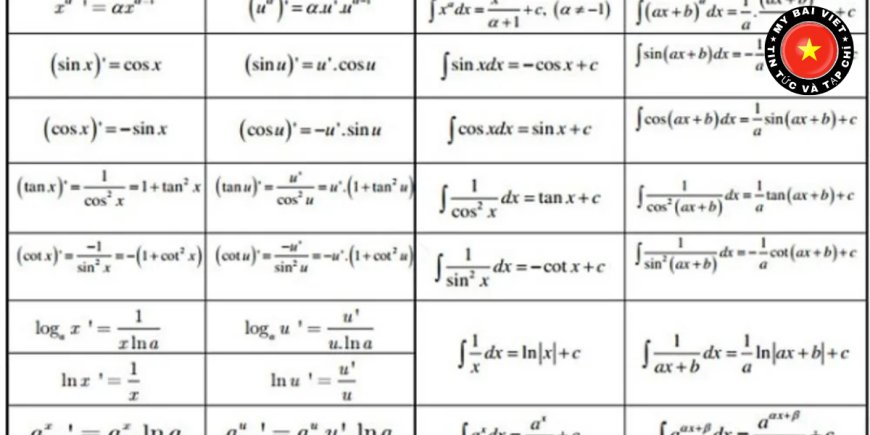
Đây là phần khiến nhiều học sinh “sợ”, nhưng nếu học đúng cách thì rất dễ nhớ.

• (sin⁡x)′=cos⁡x(\sin x)' = \cos x(sinx)′=cosx
  

• (cos⁡x)′=−sin⁡x(\cos x)' = -\sin x(cosx)′=−sinx
  

• (tan⁡x)′=1cos⁡2x(\tan x)' = \frac{1}{\cos^2 x}(tanx)′=cos2x1​
  

• (cot⁡x)′=−1sin⁡2x(\cot x)' = -\frac{1}{\sin^2 x}(cotx)′=−sin2x1​
  

👉 Nhóm công thức đạo hàm này xuất hiện rất nhiều trong bài khảo sát hàm số.
 

• (ex)′=ex(e^x)' = e^x(ex)′=ex
  

• (ax)′=axln⁡a(a^x)' = a^x \ln a(ax)′=axlna (với a>0,a≠1a > 0, a \ne 1a>0,a=1)
  

Đây là nhóm công thức đạo hàm vừa gọn vừa “đẹp”, thường được dùng trong bài toán tăng trưởng.
 

• (ln⁡x)′=1x(\ln x)' = \frac{1}{x}(lnx)′=x1​
  

• (log⁡ax)′=1xln⁡a(\log_a x)' = \frac{1}{x \ln a}(loga​x)′=xlna1​
  

Kết hợp với quy tắc hàm hợp, các công thức đạo hàm logarit có thể xử lý rất nhiều dạng bài khó.
 

Học sinh nên tự lập bảng tổng hợp công thức đạo hàm gồm:

• Hàm cơ bản
  

• Hàm lượng giác
  

• Hàm mũ – logarit
  

• Quy tắc đạo hàm
  

Việc hệ thống hóa giúp ghi nhớ lâu hơn và tránh nhầm lẫn.
 

1. Hiểu bản chất, không học vẹt

Khi hiểu vì sao có công thức đạo hàm, bạn sẽ nhớ lâu hơn.

2. Học theo nhóm

Chia công thức theo từng loại hàm.

3. Luyện tập thường xuyên

Làm bài tập là cách ghi nhớ tốt nhất.

4. So sánh – đối chiếu

Ví dụ: sin → cos, cos → -sin.
 

• Quên đạo hàm hàm bên trong
  

• Sai dấu “–”
  

• Nhầm công thức phân thức
  

• Áp dụng sai quy tắc hàm hợp
  

Nhận diện lỗi giúp bạn sử dụng công thức đạo hàm chính xác hơn.
 

Không chỉ trong Toán học, công thức đạo hàm còn được ứng dụng trong:

• Vật lý (vận tốc, gia tốc)
  

• Kinh tế (tối ưu lợi nhuận)
  

• Kỹ thuật (tốc độ thay đổi)
  

• Công nghệ (machine learning, AI)
   

Trong đề thi:

• Chủ yếu là đạo hàm cơ bản và hàm hợp
  

• Ít đánh đố, tập trung vào kỹ năng
  

• Ai nắm chắc công thức đạo hàm sẽ làm nhanh hơn
   

Công thức đạo hàm là phần kiến thức cốt lõi của giải tích, đóng vai trò quan trọng trong học tập và thi cử. Việc hiểu rõ bản chất, ghi nhớ có hệ thống và luyện tập thường xuyên sẽ giúp bạn làm chủ phần này một cách dễ dàng.

Chỉ cần nắm vững công thức đạo hàm, bạn đã đi được hơn một nửa chặng đường trong chương trình Toán THPT.